Hurricanes, climate change, and social welfare: evidence from the Caribbean
Abstract
We examine whether Caribbean islands will be worse off as hurricane activity alters under climate change. To this end, we construct island level damages for synthetic storm tracks generated from four climate models under current and future climate settings. Using a flexible stochastic dominance preference ordering framework, we find that the fat-tailed and uncertain nature of the distribution of storms makes it difficult to conclude that the region will be worse off under climate change, and is likely to depend on the degree of adaptation.
Introduction
Tropical storms have caused over 800 USD billion in damages over the last 20 years, with 58 billion due to the 2018 season alone.Footnote 1 Given the predicted increase in global temperatures due to anthropogenic influences, an obvious concern is whether such global warming will also translate into greater and/or more destructive tropical storm activity. While historical data is believed to be too limited to draw any clear conclusion in this regard (Knutson et al. 2019a), there is much more confidence in terms of making predictions from climate models. More specifically, current evidence from state-of-the-art models seems to suggest that globally the average intensity will increase by about 5%, and the proportion of higher intensity (Category 4 and 5) storms will rise 13% (see Knutson et al. 2019b), but it is not clear whether there will also be a greater frequency of tropical storms in general or the more intense ones. Thus, at least as current science stands, how climate change will affect tropical storms in the future remains a complex issue.
The likely multifaceted changes, or lack thereof, in tropical storm activity due to climate change beg the obvious question of whether these will lead countries and regions to be worse off than under current climate. A common approach to investigate how climate change affects the welfare of current and future generations in a variety of settings is to specify a social welfare function that values consumption intertemporally, as for instance is done in the well-known Dynamic Integrated Climate-Economy model (DICE) model (Nordhaus 1993) and (Millner and McDermott 2016).Footnote 2 Crucial in these welfare functions is the choice of the rate of risk aversion, measuring how society’s marginal utility changes with changes in consumption, and the social discount rate, which determines the manner in which society values current versus future consumption. Moreover, there has been a debate about the appropriate functional form of welfare itself (Pindyck 2011). However, the very nature of tropical storms and how climate is likely to manifest itself in changing their distribution over time makes using such social welfare functions for preference ordering a challenging task. Firstly, tropical storm intensity and the implied damages tend to follow a fat-tailed distribution, with many low intensity, low damaging events, and a few substantially more improbable, but nevertheless non-negligible, high intensity, high damaging storms.Footnote 3 But the degree of risk aversion will be crucial in determining how sensitive welfare is to the latter, an argument vehemently made by Martin Weitzman in the context of consumption damages due to global warming (Weitzman 2009). Secondly, evidence suggests that any climate signal will only appear in the distribution of storm activity very slowly (see Crompton et al. 2011). This potentially places additional importance, compared with common climate change contexts, on the choice of how one discounts the future relative to the present in determining whether a society will be worse off due to hurricane damages when climate changes.
Despite the importance for decision-making regarding national and international disaster management policies, as of date there is no study that has explicitly examined whether countries or regions might be worse off due to possible changes in tropical storm damages as a consequence of climate change. In this paper, we set out to undertake this task using the case study of Caribbean islands. More specifically, we use large sets of synthetic hurricanes generated from four climate models under current and future climate to generate distributions of damages due to these storms in the region. This is done by constructing local exposure within-island maps, calculating local maximum wind speed experienced for each synthetic storm, and translating these into island level damages. We then generate hypothetical distributions of annual series of damages over time, where we allow the climate signal to emerge in the storm distributions gradually. With this data at hand, we employ the time-stochastic dominance preference ranking framework developed by Dietz and Matei (2016) to explore what sets of utility functions and discount rates allow one to potentially rank hurricane damages under future relative to current climate for the Caribbean region. We extend the class of applications of this framework to examine whether climate change leaves societies worse off rather than comparing different policy scenarios as was done in its original application.
Arguably, the Caribbean is an ideal case study to investigate the welfare implications of tropical storms under climate change. Located in the North Atlantic Ocean Basin, the region is subject to considerable tropical storm activity every year. In this regard, damages due to tropical storms have been substantial over the last two decades, where estimates suggest these to have been over 10 USD billion since the year 2000.Footnote 4 Since most Caribbean islands are small in size, the impact of these damages tends to be large relative to the size of their economy. For instance, damages due to Hurricane Ivan in 2004 are estimated to have been over 200% of Grenada’s Gross Domestic Product (OECS 2005). Moreover, as small open economies, the indirect effects are also likely to be large because they are reliant on a few sectors that tend to be highly vulnerable to tropical storms, such as tourism and agriculture, for their income generation.Footnote 5 Finally, most islands in the Caribbean are heavily indebted with little access to capital markets in order to finance any ex-post rebuilding efforts (Ouattara and Strobl 2013). As a matter of fact, evidence using historical data indicates that such storms can have large net impacts on Caribbean economies (see Strobl 2012; Bertinelli and Strobl 2013). Thus, if anywhere, one would expect the Caribbean to be potentially affected by any changing tropical storm activity under global warming.
While a number of authors have investigated what economic effect tropical storms will have under climate change globally (Pielke 2007), in the USA (Emanuel 2011), and in China (Ye et al. 2019), there is currently only one study that does so for the Caribbean. More specifically, Moore et al. (2017) in a simplistic approach estimate how Caribbean countries’ GDP is affected by a hurricane’s intensity historically and then use how this intensity is linked to global temperature to predict damages under different climate change scenarios. Their analysis reveals that by 2100 cumulative economic effects are likely to be between 350 and 520 million USD. Importantly, however, none of the existing studies, for the Caribbean or elsewhere, have made welfare comparisons in terms of the impact of tropical cyclones under different climate change scenarios.
The remainder of the paper is organized as follows. In the next section, we outline the time-stochastic dominance preference ordering framework by Dietz and Matei (2016), as well as our construction of damages from tropical storms. Section 3 describes the various data sets employed in the analysis. Results are described in Section 4 and further discussed in Section 5. Finally, we provide concluding remarks in Section 6.
Methods
Welfare analysis
In order to conduct our welfare analysis we adopt the approach pioneered by Dietz and Matei (2016). More specifically, the authors extended the stochastic and almost stochastic dominance methods of preference ranking within a dynamic framework. Here we simply outline the application of this approach within our hurricane damage context, and refer the reader for full details and proofs to Dietz and Matei (2016).
Time-stochastic dominance
Assume there is a given climate scenario X under which hurricanes produce a stream of random annual damages dx ≥ 0, defined on some finite interval [0, a]. We assume also that there is a representative expected utility maximizer who consumes her deterministic income, I, net of stochastic hurricane damages x = I − dx. Net income will itself thus be a random variable that has a probability distribution f(x) and a corresponding cumulative distribution F(x).
Utility is assumed to be additively separable and discounted over time t = 0, … , T via a discount function q(t).The net present value of the stream of expected values of net income x is then: ∫T0q(t)[∫I−aIu(x)f(x,t)dx]dt=∫T0q(t)EFu[x(t)]dt (1)
where EF is expected utility integrated over x. Let us further restrict the welfare maximizer’s utility function to belong to a set of non-decreasing functions u′(x)≥0. We restrict q′(t)<0
so that there is always positive time preference in that the welfare maximizer places more value on the present than the future.
Let us consider another climate scenario Y with a stream of random damages dy ≥ 0 due to hurricanes defined on some finite interval [0, b], so that net income under Y has a probability distribution g(y), and corresponding cumulative distribution G(y). The net present value of this scenario can then be described analogously to (1). In this context one can define the preference relation between scenario X and scenario Y in terms of what Dietz and Matei (2016) coin as X time stochastic first-order dominating Y. More specifically, scenario X Time Stochastic First-order Dominates (TSFD) scenario Y iff: ∫T0q(t)EFu[x(t)]dt≥∫T0q(t)EFu[y(t)]dt,∀t∈[0,T] (2)
Intuitively, (2) implies that any impatient planner (q′(t)<0) with monotonic non-decreasing preferences (u′(x)
) will prefer hurricane damage scenario X to scenario Y as long as the integral over time of the cumulative probability function F(x) is at least as large as its counterpart for Y, i.e., G(Y ), for all net income over the whole time horizon, but strictly larger somewhere over the time horizon.
One can further restrict the above set of utility functions to additionally display (weak) risk aversion, i.e., u′′(x)≤0
. Welfare preference can then be defined in terms of the weaker time-stochastic second-order dominance. More precisely, hurricane damage scenario X will Time-Stochastic Second-order Dominate (TSSD) scenario Y iff: ∫I−aI∫T0q(t)EFu[x(t)]dt≥∫I−bI∫T0q(t)EGu[y(t)]dt,∀t∈[0,T] (3)
where (3) comes from simply integrating (2) again over x. Intuitively, one is comparing the distribution in the differences in the cumulative distribution functions F(X) and G(Y ) in order to establish TSSD.
Almost time-stochastic dominance
Unfortunately, even very small violations along the stream of damages can lead to a rejection of time first- or second-order stochastic dominance in (2) and (3). In this regard, Leshno and Levy (2002) developed the theory of almost stochastic dominance where one places restrictions on the derivatives of the utility function to exclude certain extreme preferences. Dietz and Matei (2016) extend this to the case of the time-stochastic dominance setting in that they also place restrictions on the discount function.
Assume a case where there are some violations along the distribution of hurricane damages x and y so that TSFD does not hold. However, define two parameters, 𝜖1T, where 0 < 𝜖1T < 0.5, and γ1, that characterize the degree of these violations. Dietz and Matei (2016) show that if there exists a set of utility and discount functions where the ratio between the maximum and minimum marginal utility u′(x) is less than equal 1ϵ1T−1 and the ratio between the maximum and minimum product of −q′(t)u′(x) is less than or equal to 1γ1−1, then the scenario of X can be said to almost time-stochastic first-order dominate (ATSFD) scenario Y. Importantly, these restrictions also have some intuitive interpretation. In terms of the restriction on u′(x) extreme concavity/convexity is ruled out. As an example, Dietz and Matei (2016) note that for the common constant relative risk aversion utility function this implies that the absolute value of the elasticity cannot be too large. Additionally, as ϵ1T→0.5, the utility function becomes linear. With regard to the restriction on −q′(t)u′(x)
, this tends to exclude all combinations of extreme concavity or convexity of the utility and discount functions somewhere on their respective domains. One may want to note that Pottier (2015) additionally derived properties for ATSFD for the specific case of the commonly used constant relative risk aversion utility function with marginal utility of consumption of η and an exponential discount factor with a discount rate ρ. Within our context, assuming there is no variability in initial hurricane damages and that the time period of consideration is long enough, then one can use Pottier’s (2015) results to show that there is a plane of feasible combination of ρ and η satisfying ATSFD.
Extending ATSFD to almost time-stochastic second-order dominance (ATSSD), requires three explicit restrictions on the set of feasible utility and discount functions, as characterized by a further set of violation degree parameters 𝜖12, γ1b, and γ1,2. Firstly, the ratio between minimum and maixmum u′′(x) needs to be bounded by 1ϵ12−1, where 0 < 𝜖12 < 0.5. In other words, at terminal time T large changes in u′′(x) are excluded. Secondly, the ratio of the maximum and minimum q′(t) is bounded by 1γ1b−1, thus prohibiting large changes in q′′(t). Finally, for all combinations of these restricted utility and discount functions the ratio between the maximum and minimum of q′(t)u′′(t) is bounded by 1γ1,2−1
.
Hurricane damages
Wind field model
We assume that hurricane damages depend on the local maximum wind speed during a storm as well as local assets exposed. To model local maximum wind speed v experienced during a hurricane we apply the Boose et al. (2004) version of the well-known Holland (1980) wind field model, according to which the approximate maximum local wind speed at any point i, for storm k, at hour h is given by: vik=maxh∈k(GF[Vmax,kh−S(1−sin(Tikh))vikh2]×[(Rmax,khRikh)Bkhexp(1−[Rmax,khRikh]Bkh)]12) (4)
where Vmax is the maximum sustained wind velocity anywhere in the storm k at time h, T is the clockwise angle between the forward path of the storm and a radial line from the storm center to the point of interest i, Vh is the forward velocity, Rmax
is the radius of maximum winds, and R is the radial distance from the center of the tropical storm to point i. G is the gust factor, and F, S, and B are the scaling factors for surface friction, asymmetry due to the forward motion of the storm, and the shape of the wind profile curve, respectively, and we set these parameters as in Elliott et al. (2015).
Damage function
As is common, we model the damage due to a hurricane as dependent on the degree of local wind speed experienced.Footnote 6 In terms of the actual functional form, Emanuel (2011) points out that there are energy dissipation reasons to assume that the relationship between wind speed experienced and damage incurred is to the cubic power. Moreover, there is unlikely to be any damage for winds that fall below 92 km/h. In the spirit of Emanuel (2011), we incorporate these features and ensure that the percentage of damage varies between 0 and 1 with the following damage function of storms k = 1…, K during time period t for location i on island m: fimt=∑k∈tv3imk1+v3imk (5)
where vimk=MAX[(vimk−vthresh),0]vhalf−vthresh (6)
where vikt is the maximum wind speed of storm k experienced at point of interest i on island m during year t, vthresh is the threshold below which no damage occurs, and vhalf is the threshold at which half of the property is damaged. Following Emanuel (2011), we assume values of 92 km/h and 204 km/h for vthresh and vhalf, respectively. One should note that (5) is defined in terms of the percentage of damage caused per storm. Since feasibly any location i could be hit by several storms within a year, we assume here that damages are cumulative but cannot exceed 100% in a given year.Footnote 7
In order to arrive at island, and ultimately Caribbean level, damages for each year, we aggregate local damages in the following manner: damagest=−∑m∈MM∑i∈IIwim×ASSETSmt×fimt;∑i∈mmwim=1 (7)
where ASSETS are the total potentially damageable assets in island m and w is the share of these assets in location i.
Simulated hurricane damage distributions over time and climate
We can use (4) through (7) to derive Caribbean wide damages for a set of storms occurring during a given year. We do so for the sets of synthetic storms generated from four different climate models under current and future climate scenarios (20th century and RCP 8.5), described in detail in Section 3.2 below. In order to generate distributions of such damages over a given time horizon we proceed as Emanuel et al. (2012). More specifically, we first, for each climate model and each climate scenario, generate a 1000 100-year time series of hurricane damages by randomly generating from a Poisson distribution the number of events, where the mean storm frequency is given by the climate models and scenarios for that simulated year. We then randomly choose this number of storms from each given climate model and climate setting set. While the time series for the 20th century weather are taken to represent simulated storms over 100 years under that setting, in order to incorporate a realistic future evolution of damage distribution in which a global warning signal gradually emerges over time, we follow the approach by Emanuel (2011). More precisely, we blend each pair of 20th and RCP 8.5 damage series during one of the 1000 simulations into a single combined time series by merging these together using as weight the linear time passed (1–100), where the weight on the RCP 8.5 grows as time passes. This in essence allows the distribution of hurricanes of the future climate to become more prominent as one extends time into the future. As noted by Emanuel (2011) and similar to Crompton et al. (2011), this assumes that the noise surrounding a global warming signal is not due to multi-decadal variability, but rather random variability on time scales ranging up to a few years. Thus the noise would also include ENSO-related variability, which is a well-known driver of short-term variation in hurricane activity (see Goldenberg 2001). As a comparison we alternatively also allowed the signal to evolve in a cubic manner with time.
Data
Study region
Our study region consists of islands within the Caribbean Sea, which itself is located within the North Atlantic Ocean Basin. The total number of islands in this region is 28, of which 13 are sovereign states and the others dependent territories: Anguilla, Antigua and Barbuda, Aruba, Bahamas, Barbados, Bermuda, Bonaire, Saint Eustatius and Saba, British Virgin Islands, Cayman Islands, Cuba, Curacao, Dominica, Dominican Republic, Grenada, Guadeloupe, Haiti, Jamaica, Martinique, Montserrat, Puerto Rico, Saint Kitts and Nevis, Saint Lucia, Saint Vincent and the Grenadines, Saint-Barthelemy, Saint-Martin, Sint Maarten, Trinidad and Tobago, Turks and Caicos Islands, and US Virgin Islands.
Synthetic hurricane tracks
Synthetic hurricane tracks were kindly generated under different climate models and scenarios by Kerry Emanuel using a statistical/deterministic hurricane model developed in Emanuel et al. (2008). More specifically, this approach uses kinematic and thermodynamic statistics derived from a climate model to generate synthetic tropical storms. One should note that Emanuel et al. (2008) show, using the period 1980 to 2006, that the storms simulated had reasonable agreement with historical storms, including their spatial and temporal variability on time scales from seasons to decades. Moreover, particularly for the North Atlantic Basin, in which the Caribbean islands lie, the interannual variability of storm frequency responded reasonably well to ENSO and is highly correlated with observed interannual variability. One weakness might be that the local genesis maximum in the Caribbean was to the southeast of the observed maximum, although, as Emanuel et al. (2008) point out, this discrepancy may well have been due to sampling, since the number of synthetic events was six times more than the number of observed storms in the region during the time period under consideration.
For the context here, 4000 events were generated for four CMIP5 models within the relevant vicinity of our study region, under both 20th century simulations (1981–2000 weather) and future (2081–2100) RCP 8.5 pathway simulations.Footnote 8 The four CMIP5 climate models used were MIROC5, MRI5, IPSL5, and CCSM4, which are climate models developed by different institutions (see Emanuel et al. 2008for details). For each of these eight simulations, the frequency of events is calibrated based on the observed frequency during the period 1981–2000. The set of synthetic storm events are then fed into the hurricane wind field and damage function models described above to generate Caribbean wide damages for each storm.
Income
As a measure of income we use the sum of latest available GDP for all islands in our sample. These were collected from a variety sources, including the World Penn Tables, World Bank Indicators, and national sources when they were not available from the former two. In order to predict income in the future we take the predictions from Leimbach et al. (2017), who provide annual GDP growth rate predictions for five different shared socio-economic pathways (SSP) for low, medium, and high income countries up 2100. Give that a majority of the Caribbean islands are classified as high income and all others upper middle income countries according to the recent (2020) World Bank classification, we use the average growth rates for the high income group for the medium growth rate scenario SSP3, namely 0.75% per year.
Island asset exposure
In order to proxy the island level asset exposure in monetary terms, i.e., ASSETS, in (7), we use the exposure data from the Caribbean Catastrophe Risk Insurance Facility (CCRIF)’s second-generation hazard and damage model (CCRIF 2019). This exposure proxy is generated from population data and land cover information in order to infer construction types and non-residential exposure. Estimation of the infrastructure is based on the density and distribution of building types, while the agricultural component in the damage estimation is estimated using land cover data and the agriculture’s contribution to a country’s GDP. In order to predict exposure for the future, we as a benchmark assume that it grows at the same rate as GDP and thus use the same annual growth rate described above (0.75%).
Of course, assuming that island level exposure and hence damages increase at the same rate as income implies that the income elasticity of damage is unitary, and hence that no adaptation is taking place. Bakkensen and Mendelsohn (2016) examined this issue by relating tropical cyclone damages to income across the globe and found that this elasticity depended on factors such as the level of income and whether areas were rural or urban. In order to crudely incorporate adaptation, or the lack thereof, in our analysis we alternatively allow exposure to increases at lower and higher rates than GDP, indicating positive and negative adaptation, respectively, for the climate change scenarios. To do so, we use the range of estimates of how damages responded to changes in income from Bakkensen and Mendelsohn (2016), where the lowest (for high income areas) indicated a 82% smaller increase and the highest (for urban areas) a 216% greater increase in damages in response to a unit increase in GDP. We allow exposure to increase at corresponding rates with income increase to create demonstrative counterfactuals of positive and negative adaptation at the extreme end of historically observed possibilities.
Local exposure weights
Unfortunately we do not have local asset exposure maps for individuals islands. However, recently a number of researchers across several disciplines have used remote sensing measures as a proxy for local economic wealth and population (see Zhao 2019 for a review). We thus distribute total island level asset values by using high-resolution satellite-derived nightlight intensity as a proxy for local assets. To this end, we resort to the nightlight intensity measures derived from the Defense Meteorological Satellite Program (DMSP) satellites. More specifically, we use the 2013 stable, cloud-free value of the percentage of nightlight occurrences for each pixel normalized across satellites to a scale ranging from 0 (no light) to 63 (maximum light) (see Elvidge et al. 1997). In order to construct local exposure w in (7) we simply calculate the share of each grid’s intensity in total island intensity. Importantly, the grid cell centroids also serve to define the individual locations i for which we calculate the local damages due to storms as outlined above.
Results
Hurricane damage distributions and trends
We depict the distribution of the stream of annual hurricane damages over the whole time period t = 0, … , 100 for the four climate models under the 20th century and RCP 8.5 scenarios in Fig. 1 as quantile-quantile plots.Footnote 9 As can be seen, for all four climate models most damages are zero or fairly small, generally less than 50 billion USD. As a matter of fact, zero damage years under current (future) climate constitute 52 (48), 58 (41), 50 (29), and 36 (29) per cent for the CCSM4, IPSL5, MIROC5, and MRI5 models, respectively. If one considers the mean average annual damages due to hurricanes then the CCSM4, IPSL5, MIROC5, and MRI5 models predict these to be 0.6 (0.7), 0.9 (1.7), 1.2 (3.0), and 2.0 (3.0) for current (future) climate, respectively. Thus, relative to the total exposed assets in the Caribbean (2,257 billion USD), expected percentage damaged per year is small, ranging from 0.03 and 0.13%. Considering the largest damaging years in our synthetic set, which by construction have a return period of 10,000 years, damages under these climate models would, respectively, be 110 (147), 136 (248), 172 (401), and 303 (452) billion USD for current (future) climate. This constitutes a range of between 5 and 20% of total assets in the Caribbean being destroyed for such events.
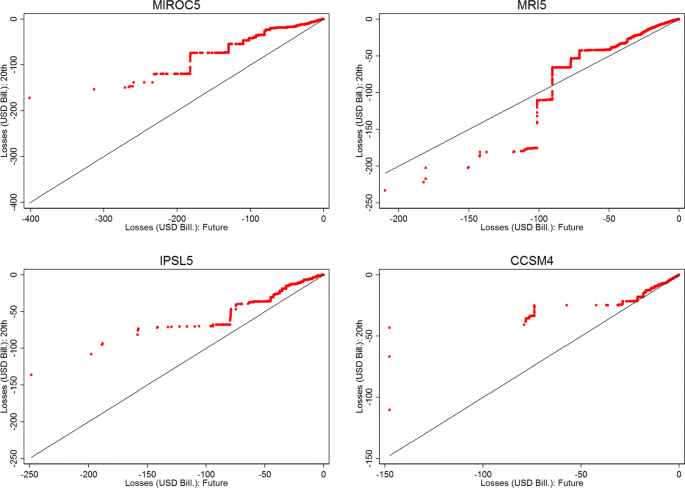
Comparing the two different climate outcomes, one finds that for smaller damages the 20th Century climate hurricane annual damage distributions all lie to the right of the reference line, although not completely for the CCSM4 model. This suggests that smaller damages are relatively more likely than under future climate. Comparing the quantiles for larger damages, it becomes apparent that these are fairly infrequent regardless of climate model or climate scenario, but still of non-negligible probability. For three of the models—MIROC5, IPSL5, and CCSM4—these large, but low probability, annual damage years are much more common under future climate. The exception in this regard are the damages generated from hurricanes under the MRI5 model, where damages above 80 USD Billion constitute a larger proportion of the total distribution under current climate.
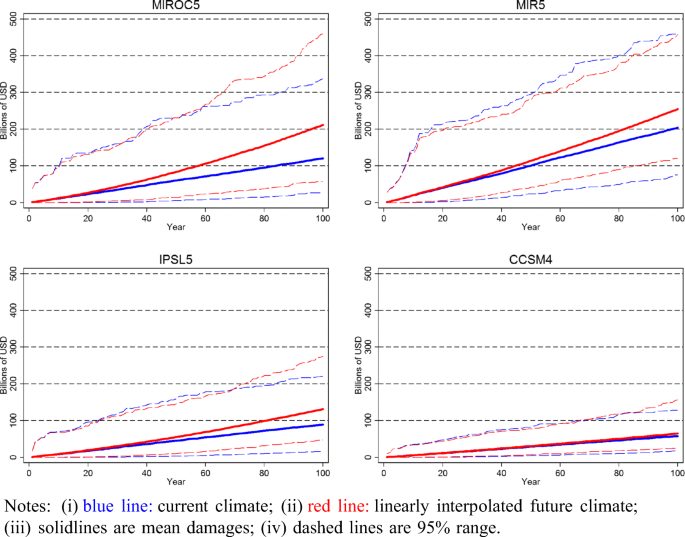
The depiction of damages in Fig. 1 of course ignores their time dimension. We thus in Fig. 2 show the evolution of mean cumulative damages, including the 95% range across simulations, over time for each of our four climate models for the 20th climate and RCP 8.5 contexts, where for the latter we assume that the climate signal emerges linearly with time as outlined in Section 2.3. Under all four climate models, mean average cumulative damages increases more over time under future climate. This is most prominent for the MIROC5 model, while it is substantially less pronounced for the CCSM4 model series. In this regard, average (across simulations) cumulative damages over a 100 years for the former would be in the region of 90 billion USD higher under climate change, but only be 7 billion lower for the latter. Importantly, however, for all four models, the 95% range of estimates of cumulative damages is fairly wide. For example, for the MIR5 model, cumulative damages after a 100 years under climate change could range between 149 and 459 billion USD. Even for the CCSM4, which shows the lowest variability, the range for future (current) climate damages falls between 32 (26) and 115 (99) billion USD. Nevertheless these numbers are much larger than those found by Moore et al. (2017), who discovered a range between 350 and 520 million USD. This is likely due to the fact they did not actually use a set of hypothetical storms under different climate scenarios, and consequently did not explicitly model damages. Rather they used an estimated historical relationship between GDP and a power index of storms, as well predictions in this power index from global temperature changes under climate change, to infer future impacts.
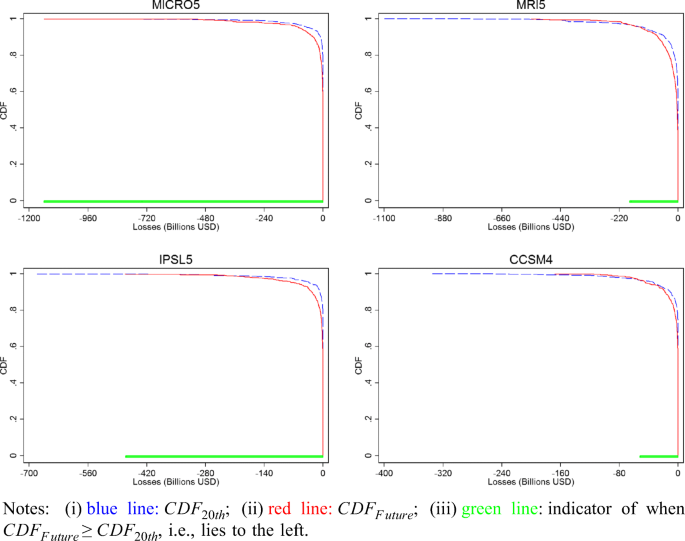
In order to get a better picture of the distribution of hurricane damages over time we also depict the cumulative distribution functions (CDF) of these for current and future climate for our four climate models at snapshots t = 50 and t = 100 in Figs. 3, and 4, respectively, where the blue (red) line refers to the cumulative probability distribution of current (future) climate. Additionally, at the bottom of each graph we also include a green line indicating up to which point on the damage range current climate damages lie to the left of the future climate damages.
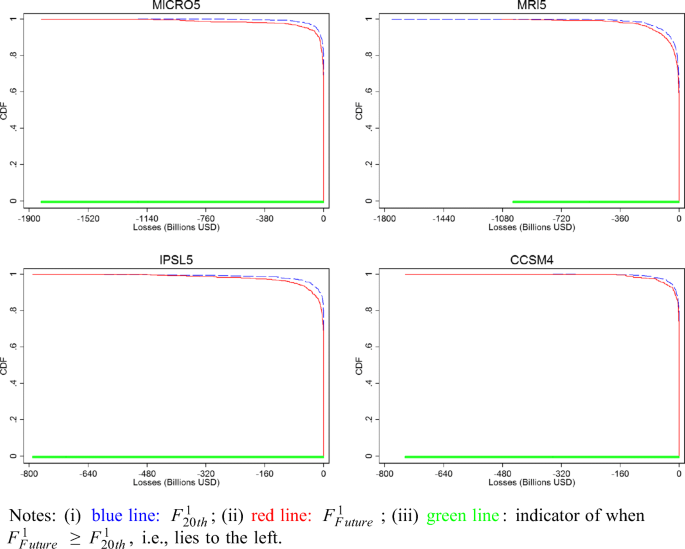
and F120th at t = 100. (i) blue line: F120th; (ii) red line: F1Future; (iii) green line: indicator of when F1Future≥F120th
, i.e., lies to the leftFull size image
Examining the CDFs at 50 years (Fig. 3), it is apparent that for all models, except MIROC5, the distributions cross at some stage. This suggests that at t = 50 under the current climate conditions hurricane damages are relatively more characterized by high damage low probability events than the distribution of damages under future climate for most models. In contrast, at t = 100 (Fig. 4) the picture is reversed, where for all models except MRI5 the CDF of future climate now lies to the left of that of 20th climate. Taken together, the two time snapshots of relative CDFs suggest that over time future climate becomes more characterized by high damage low probability events rather than high probability low damaging storms than under current climate conditions.
Time-stochastic order dominance tests
Time-stochastic first- and second-order dominance
The results of the time-stochastic dominance tests for three terminal periods (50 and 100 years) and our four climate models are given for a linear signal and where exposure grows at the same rate as income in the upper panel of Table 1. Accordingly, for all models, for all terminal periods, pure time-stochastic first-order (TSFD) and second-order (TSSD) dominance fail. This may not be surprising given the results regarding the cumulative distributions F1 and F2 at various points in time as just described. Table 1 Stochastic dominance testsFull size table
Almost ideal stochastic first-order dominance
The restriction placed on the utility function, i.e., 𝜖1T, in order to achieve almost time first-order stochastic dominance (ATFSD) are shown in the 7th column of the first panel in Table 1 for a linear (LIN) climate signal. If one chooses terminal time T = 50, 𝜖1 is found to be relatively large—ranging from 0.06 to 0.46—across all models, although still below the 0.5 threshold. At time T = 100, however, all models experience a fall in the parameter, which is just the share of the violations at the terminal period. As a matter of fact, for the MIROC5 model, this parameter reduces to zero.
In the 8th column of Table 1, we depict the restriction on the product of the utility and discount function marginals. These differ across models, with the lowest restrictions for the MIROC5 model, and the highest for the CCSM4 model, regardless of the choice of terminal period T. For all four models, as one increases the terminal period, the size of γ1 falls, thus increasing the set of admissible utility and discount functions.
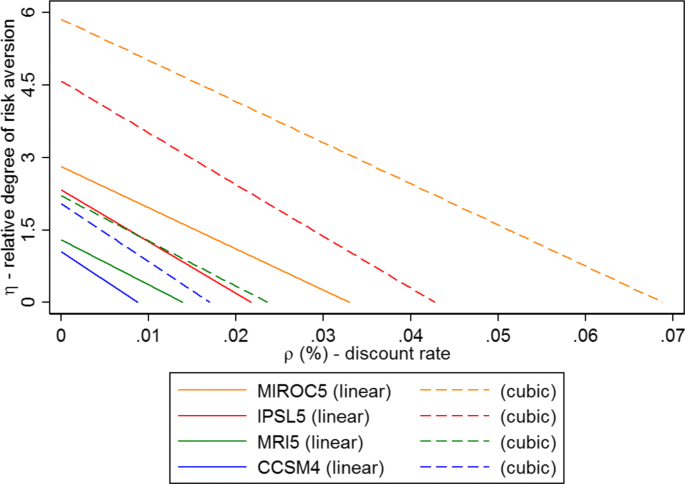
We depict the spaces of feasible sets of elasticities of the marginal utility of consumption (η) and discount rates (ρ) under a CRRA utility function under ATFSD at T = 100 in the spirit of Pottier (2015) with a linear climate signal as solid lines in Fig. 5. One should note in this regard that the feasible set includes all possible pairs beneath the given lines. Accordingly, for all models only extremely small discount rates are feasible in order for hurricane damages under current climate to be preferable to a setting under climate change. This set is largest for the MIROC5 (up to 0.033%) and lowest (up to 0.009%) under the CCSM4 model. In terms of η and assuming a zero discount rate, the highest admissible elasticity of the marginal utility of consumption ranges from 1.2% (CCSM4) to 3.0% (MIROC5).
Almost ideal stochastic second-order dominance
Even if ATFSD cannot be achieved, under less restrictive criteria one might still be able to obtain preference ranking by invoking ATSSD. In the final three columns of the first panel in Table 1, we provide the estimated parameter restrictions for ATSSD. Considering the space of decreasing pure discount functions and non-decreasing, weakly concave utility functions, the restriction (γ1,2) for all four models falls as one increases the time of the terminal period. As a matter of fact, for the MIROC5 and CCSM4 model, this restriction is not binding by the time 100 years have passed. Examining, 𝜖2T, one finds nevertheless that the set of admissible u will be bounded, but again, as one considers a further period in the future this condition becomes less restrictive. Regardless of the time horizon, it is least bounding for the MIROC5 and most restrictive for the CCSM4 model. Finally, the remaining restriction on the first-order condition of the discount function, i.e., γ1b, is not binding for the IPSL5, MIROC5, and MRI5 models, regardless of the the time horizon. It is only restrictive for the CCSM4 model, but with some variability according to the choice of T.
Cubic climate signal
We repeated all stochastic dominance tests for the setting where we allow the climate signal to emerge in a cubic manner with time (CUB). The results of these are shown in the second panel of Table 1. Accordingly, as before strict time-stochastic first- or second-order stochastic dominance are not achieved under any of the climate models. In terms of their almost counterparts, generally the estimated parameters under a cubic climate signal imply a less restrictive set of utility functions, discount functions, and the product of the marginals of the utility and discount functions for both ATFSD and ATSSD. Examining the set of admissible implied values of the elasticity of marginal consumption and the time discount rate at T = 100 for a constant relative utility function with exponential discounting, Figure 5 shows a similar pattern in terms of which models provide a greater set of elasticity and discount rate pairs for the cubic climate signal model (depicted as dashed lines). The actual sets are substantially larger though, generally about twice in value.
Adaptation
The results of allowing positive (+) and negative (-) adaptation by letting exposure increase at lower and higher rates than income, respectively, are presented in the last two panels of Table 1. As for the case of zero (0) adaptation, under positive adaptation, neither TFSD nor TSSD is achieved. Additionally the degree of violation in 𝜖1T and in the marginals of the product of the utility and discount function to rise substantially under positive adaptation. As a matter of fact, except for the MIROC5 model and the IPSL5 model at T = 50, all estimated values of this parameter are above the permissible threshold of 0.5, eliminating the possibility of ATFSD. Examining the restrictions on ATSSD shows that except for the MIROC5 model there also exists no admissible set of utility functions, regardless of model or terminal period. Even for the MIROC5 model the violations on the discount rate and the marginals of the utility and discount functions appear high enough to suggest that the space for agreement will be limited.
The findings from the assumption of exposure increasing at a greater rate shown in the last panel of Table 1 suggest that there is no case in which there is TFSD. Nevertheless for all models the estimated violation parameters are small enough to indicate a larger set of admissible utility and discount functions to achieve ATFSD than under zero adaptation. As a matter of fact, using Pottier’s (2015) framework suggests the plane of admissible degrees of risk aversion and discount rates to be contained within ranges between 3.5 and 10.3 and 0.06 and 0.16, respectively. In contrast, TSSD is achieved for all models except for MRI5 at T = 100. However, even for the latter the only restriction needed to achieve ATSSD is in terms of the utility function and the value of the estimate on 𝜖2T indicates that there is a large set of non-decreasing utility functions displaying weak risk aversion that will be able to do so.
Discussion
Using sets of synthetic storm tracks under different climate models and current and future climate settings, we simulated the distribution of annual damages due to hurricanes in the Caribbean. This showed that under all models and both climate settings, most years experience zero or small amounts of damages, so that the average expected damage is small, i.e., well below 1%, although these are expected to be slightly larger on average under climate change. Nevertheless, large damages, causing up to 20% damages in total assets, cannot be ruled out, and for three of the four models these tended to be more likely under future climate. One may want to note that such fat-tailed distributions of damages are typical of extreme climate events like tropical storms (Chavas et al. 2012). Constructing 100 year time series where a climate signal emerges linearly in time in tropical storm activity, our findings show that differences in mean cumulative damages only gradually become relatively larger under the setting where climate changes, but that the strength of this difference is very model dependent. Moreover, there is a large amount of uncertainty around the actual path that cumulative damages under current and future climate could take. Considering these features of the simulation in terms of whether the Caribbean will be worse off under climate change, one is faced with two interlinked aspects to consider: (i) how to weight expected small hurricane damages against improbable, but non-negligible, large damages, and (ii) how to value the future relative to the present for streams of damages over time. In essence, (i) is a question of the welfare function that is being maximized, and (ii) with what rate to discount the future.
Stochastic dominance is a potentially convenient tool to make decisions in terms of preferential ordering in the face of uncertainty, and has more recently been developed to also be employed in inter-temporal settings (Dietz and Matei 2016). However, despite its flexibility in terms of only making minimum assumptions regarding the set of plausible underlying preferences and how to discount the future, violations leading one to being unable to draw any conclusions in terms of what situation is preferred over another are likely. As a matter of fact, when we assumed no adaptation, neither in time first order nor in the less restrictive second order, stochastic dominance tests did not allow us to draw any clear conclusions in terms of whether the Caribbean would be worse off under climate change, regardless of the time horizon we chose. This may not be surprising given the fat-tailed nature of the distribution of damages and that any climate signal was assumed to emerge only slowly.
Placing restrictions on the extent of violations under temporal stochastic dominance tests nevertheless allowed us to describe a set of admissible, but more restrictive, utility and time discount functions that could lead to preference ordering. In this regard, if one considers a relatively short-time horizon of 50 years, for most climate models the implied set of utility functions that would allow ranking under almost time-stochastic first-order dominance was not too far from being restricted to risk neutrality, and well below what laboratory experiments suggest are feasible. More precisely, in a laboratory experiment of investment preferences (Levy et al. 2010) found that admissible values of 𝜖1 ranged between 0.03 and 0.06, while this parameter for four of our climate models was found to be between 0.46 and 0.9. Using a 100 year time horizon, in contrast, did push the parameter to be within this range of realistic values.
Considering both risk aversion and time discounting restrictions together within a 100 year terminal time horizon, our analysis indicated that within the set of admissible discount rates, the restriction that would need to be placed on how society values risk is mostly not important. For example, the relative degree of risk aversion has been estimated to be 1.6% for Latin American countries (Evans 2005) and 1.4% for OECD countries (Lopez 2008), and in our study the set of admissible estimates encompassed these values for two models if the discount rate was low enough. However, the set of permissible discount rates was even under risk neutrality no more than 0.032% under any of the climate models. Such a rate would imply that one would value a dollar a 100 years from now no less than 97 cents. This limit, for instance, would be much lower than what is commonly assumed in climate change contexts (see, for instance, Wang et al. 2019). As a matter of fact, using the estimated average relative degree of risk aversion, consumption growth rate, and social discount rate from Lopez (2008) for a set of Latin American countries, the Ramsey rule suggests a realistic pure rate of time preference of 0.86%, implying that a dollar in the future should be valued about 42 cents today.
Although we further relaxed how one orders preferences in a stochastic and temporal setting by looking at almost time second-order stochastic dominance, there is unfortunately no current evidence to translate these restrictions into actual sets of admissible elasticities of marginal utility of consumption or social time discount rates. The only benchmark of parameters available is an exercise undertaken by Dietz and Matei (2016), where the authors examine preferential ordering of carbon emissions under various abatement policies using a DICE model with uncertainty. The suggested restrictions they find in order to prefer any of the policies to business as usual under almost time second-order stochastic dominance tests are multiple times smaller than what we observe in our Caribbean hurricane damage setting, for both the utility and discount rate functions.
While one might suspect that the driving factor behind the restrictive nature of the discount rate in preference ordering may be due the fact that we only allowed the climate signal to emerge slowly, as previous evidence suggests is a realistic scenario, this actually is not the case. Rather, in our experiment where we alternatively allowed the signal to appear in a cubic manner so that most of the climate signal appears in the first few years, the admissible set of discount rates was also not realistic. More specifically, even if we assumed no risk aversion, the range of discount rates across models under a cubic climate signal would still have to be between 0.02 and 0.07%. Thus, the implied differences in hurricane damages under climate change with no adaptation are simply not prominent enough across our models to allow a reasonable preference ordering.
A far more crucial assumption to finding a preference ranking appears to be how one models adaptation. One should note in this regard that in the benchmark case for the results just described, we simply assumed that both income and exposure grew at the same rate, which would imply essentially no adaptation. When we crudely modeled positive adaptation by allowing exposure to grow at a lower rate than income under the climate change scenarios, this made all forms of time order stochastic dominance, whether strict or almost, even more unlikely. This is not surprising given that this setting would mean that even if storms are potentially stronger under climate change, their impact would be smaller because relatively (to income) less assets would be exposed. In contrast, if one alternatively allows for exposure to grow at what historical evidence suggests might be the lowest rate of observed negative adaptation across countries, a possible preference ranking is possible. In particular, hurricane damages under current climate for three of the models would be strictly preferred in the second-order sense, and for all models in the first-order sense, under minimum restrictions on the utility and discount functions. For the first-order sense, however, while the admissible degrees of risk aversion contained realistic values, acceptable discount rates would still need welfare maximizers to value a dollar today no less than between 85 or 94 cents tomorrow (depending on the climate model). Thus, one can conclude that welfare is likely lower under climate change only in the second-order sense.
Importantly, the possibility of exposure increasing at a relatively higher rate than income cannot to be excluded as a possible scenario for the Caribbean. More specifically, the region has a population density that is ranked among the highest in the world and biased towards the coast. Additionally, a large part of the region’s income generated depends on tourism, the attraction for which relies on much of the tourism infrastructure being close to the coast. However the coast is also the area most vulnerable to hurricane damages. Worryingly, such vulnerability is likely to increase for the Caribbean in the future (United Nations and Social Affairs 2019; Mackay and Spencer 2017).
Conclusion
We examined whether Caribbean islands would be better or worse off due to changes in hurricane damages as a consequence of global warming. Our results show that it is difficult to draw any conclusion in this regard under the assumption of no adaptation, where particularly the range of necessary time discount rates does not seem realistic. This is likely the result of the very nature of tropical storms in that climate change asserts itself in their distribution in a complex way. In contrast, allowing for greater increases in exposure of assets to hurricane damages relative to growth in income did create settings in which the status quo would generally be at least weakly preferred to that under climate change for most models.
There are of course a number of drawbacks to the analysis underlying our results that could be addressed in future research. Firstly, we only very crudely allowed for situations of no, negative, or positive forms of adaptation under climate change by simply assuming asset exposure to grow at different rates relative to income. A more careful modeling of how adaptation could take place, inclusive of explicitly specifying its nature and cost, is likely to provide more realistic settings. Secondly, our analysis was restricted to examining hurricanes in terms of wind induced damages. Although wind speed has been shown to be correlated with precipitation and storm surge, it is far from perfectly so (see, for instance, Yu et al. 2017; Needham and Keim 2014). In this regard, with rising sea levels, even if climate change were not to induce much alteration in the distribution of storms, the damages due to storm surge will certainly rise regardless. Importantly in the Caribbean much of the population and infrastructure are close to the coast by nature of the size of the islands and their attraction for tourism. One may also note that most models predict that precipitation during tropical storms is also likely to increase with global warming, thus further increasing damages (see Knutson et al. 2019a; Trepanier et al. 2017). Finally, the analysis could benefit from future investigation into how our results depend on the the damage function. As it stands, its form here was based on the well-known cubic relationship between wind exposure and damages to infrastructure, with some strong assumptions about the minimum damage threshold and functional form that could be further explored. More importantly perhaps, we did not explicitly model the indirect losses that result through disruptions to economic markets that occur as a result of the physical damages. This could, for example, be done by incorporating Inoperability Input-Output or Computer General Equilibrium models into the analysis (Al Kazimi and Mackenzie 2016).
Notes
- 1.Author’s own calculations using the EMDAT database.
- 2.The DICE model is a computer-based integrated assessment model developed by William Nordhaus that allows an assessment of the costs and benefits of combating climate change.
- 3.See, for example, Jagger and Elsner (2006) and Chavas et al. (2012) for a study of the tropical storm intensity and damages for the US.
- 4.Authors’ own calculations using the EMDAT database.
- 5.See, for instance, Granvorka and Strobl (2013) for a study of the impact on tourism, and Spencer and Polachek (2015) and Mohan (2016) for examples of the effect on agriculture in the Caribbean.
- 6.While damages from hurricanes also arise from storm surge and extreme precipitation during the event, as noted by Emanuel (2005), these tend to be correlated with wind speed of the storm.
- 7.This may overstate damages if already damaged assets within a year cannot be damaged further.
- 8.The RCP8.5 combines assumptions about modest rates of technological change and energy intensity improvements with high population and relatively slow income growth, leading in the long term to high energy demand and GHG emissions in absence of climate change policies (see Riahi et al. 2011).
- 9.For any given loss value on the x-axis, when points lie above it this implies that the probability of having losses greater than that value is greater under future climate.
References
- Al Kazimi A, Mackenzie CA (2016) The economic costs of natural disasters, terrorist attacks, and other calamities: an analysis of economic models that quantify the losses caused by disruptions. In: 2016 IEEE Systems and Information Engineering Design Symposium (SIEDS), IEEE, pp 32–37
- Bakkensen LA, Mendelsohn RO (2016) Risk and adaptation: evidence from global hurricane damages and fatalities. J Assoc Environ Res Econ 3(3):555–587 Google Scholar
- Bertinelli L, Strobl E (2013) Quantifying the local economic growth impact of hurricane strikes: an analysis from outer space for the caribbean. J Appl Meteorol Climatol 52(8):1688–1697 Google Scholar
- Boose ER, Serrano MI, Foster DR (2004) Landscape and regional impacts of hurricanes in Puerto Rico. Ecol Monogr 74(2):335–352 Google Scholar
- CCRIF (2019) Understanding ccrif: a collection of questions and answers
- Chavas D, Yonekura E, Karamperidou C, Cavanaugh N, Serafin K (2012) Us hurricanes and economic damage: extreme value perspective. Nat Hazards Rev 14(4):237–246 Google Scholar
- Crompton RP, Pielke RA Jr, McAneney KJ (2011) Emergence timescales for detection of anthropogenic climate change in us tropical cyclone loss data. Environ Res Lett 6(1):014003 Google Scholar
- Dietz S, Matei NA (2016) Spaces for agreement: a theory of time-stochastic dominance and an application to climate change. J Assoc Environ Res Econ 3(1):85–130 Google Scholar
- Elliott RJ, Strobl E, Sun P (2015) The local impact of typhoons on economic activity in china: a view from outer space. J Urban Econ 88:50–66 Google Scholar
- Elvidge C, Baugh K, Hobson V, Kihn E, Kroehl H, Davis E, Cocero D (1997) Satellite inventory of human settlements using nocturnal radiation emissions: a contribution for the global toolchest. Glob Chang Biol 3(5):387–395 Google Scholar
- Emanuel K (2005) Increasing destructiveness of tropical cyclones over the past 30 years. Nature 436(7051):686 Google Scholar
- Emanuel KA (2011) Global warming effects on US hurricane damage. Weather Clim Soc 3(4):261–268 Google Scholar
- Emanuel K, Fondriest F, Kossin J (2012) Potential economic value of seasonal hurricane forecasts. Weather Clim Soc 4(2):110–117 Google Scholar
- Emanuel K, Sundararajan R, Williams J (2008) Hurricanes and global warming: results from downscaling ipcc ar4 simulations. Bull Am Meteorol Soc 89 (3):347–368 Google Scholar
- Evans DJ (2005) The elasticity of marginal utility of consumption: estimates for 20 oecd countries. Fiscal Stud 26(2):197–224 Google Scholar
- Goldenberg SB, Landsea CW, Mestas-Nuñez AM, Gray WM (2001) The recent increase in atlantic hurricane activity: causes and implications. Science 293(5529):474–479 Google Scholar
- Granvorka C, Strobl E (2013) The impact of hurricane strikes on tourist arrivals in the caribbean. Tour Econ 19(6):1401–1409 Google Scholar
- Holland GJ (1980) An analytic model of the wind and pressure profiles in hurricanes. Mon Weather Rev 108(8):1212–1218 Google Scholar
- Jagger TH, Elsner JB (2006) Climatology models for extreme hurricane winds near the united states. J Clim 19(13):3220–3236 Google Scholar
- Knutson T, Camargo SJ, Chan JC, Emanuel K, Ho C-H, Kossin J, Mohapatra M, Satoh M, Sugi M, Walsh K, et al. (2019a) Tropical cyclones and climate change assessment: Part i. detection and attribution Bulletin of the American Meteorological Society, (2019)
- Knutson T, Camargo SJ, Chan JC, Emanuel K, Ho C-H, Kossin J, Mohapatra M, Satoh M, Sugi M, Walsh K, et al. (2019b) Tropical cyclones and climate change assessment: Part ii. projected response to anthropogenic warming Bulletin of the American Meteorological Society, (2019)
- Leimbach M, Kriegler E, Roming N, Schwanitz J (2017) Future growth patterns of world regions–a gdp scenario approach. Glob Environ Chang 42:215–225 Google Scholar
- Leshno M, Levy H (2002) Preferred by all and preferred by most decision makers: Almost stochastic dominance. Manag Sci 48(8):1074–1085 Google Scholar
- Levy H, Leshno M, Leibovitch B (2010) Economically relevant preferences for all observed epsilon. Ann Oper Res 176(1):153–178 Google Scholar
- Lopez H (2008) The social discount rate: estimates for nine Latin American countries. The World Bank
- Mackay EA, Spencer A (2017) The future of caribbean tourism: competition and climate change implications. Worldwide Hospitality Tourism Themes 9(1):44–59 Google Scholar
- Millner A, McDermott TK (2016) Model confirmation in climate economics. Proc Nat Acad Sci 113(31):8675–8680 Google Scholar
- Mohan P (2016) Impact of hurricanes on agriculture: evidence from the caribbean. Nat Hazards Rev 18(3):04016012 Google Scholar
- Moore W, Elliott W, Lorde T (2017) Climate change, atlantic storm activity and the regional socio-economic impacts on the caribbean. Environ Dev Sustain 19(2):707–726 Google Scholar
- Needham HF, Keim BD (2014) Correlating storm surge heights with tropical cyclone winds at and before landfall. Earth Interact 18(7):1–26 Google Scholar
- Nordhaus WD (1993) Optimal greenhouse-gas reductions and tax policy in the dice model. Am Econ Rev 83(2):313–317 Google Scholar
- OECS (2005) Grenada: macro-socio-economic assessment of the damages caused by hurricane ivan-sep 2004
- Ouattara B, Strobl E (2013) The fiscal implications of hurricane strikes in the caribbean. Ecol Ccon 85:105–115 Google Scholar
- Pielke RA Jr (2007) Future economic damage from tropical cyclones: sensitivities to societal and climate changes. Philosophical transactions of the royal society a: mathematical. Phys Eng Sci 365(1860):2717–2729 Google Scholar
- Pindyck RS (2011) Fat tails, thin tails, and climate change policy. Rev Environ Econ Policy 5(2):258–274 Google Scholar
- Pottier A (2015) Time-stochastic dominance and iso-elastic discounted utility functions
- Riahi K, Rao S, Krey V, Cho C, Chirkov V, Fischer G, Kindermann G, Nakicenovic N, Rafaj P (2011) Rcp 8.5—a scenario of comparatively high greenhouse gas emissions. Clim Change 109(1-2):33 Google Scholar
- Spencer N, Polachek S (2015) Hurricane watch: Battening down the effects of the storm on local crop production. Ecol Econ 120:234–240 Google Scholar
- Strobl E (2012) The economic growth impact of natural disasters in developing countries: evidence from hurricane strikes in the central american and caribbean regions. J Develop Econ 97(1):130–141 Google Scholar
- Trepanier J, Yuan J, Jagger T (2017) The combined risk of extreme tropical cyclone winds and storm surges along the us gulf of Mexico coast. J Geophysic Res Atmos 122(6):3299–3316 Google Scholar
- United Nations DoE, Social Affairs PD (2019) World population prospects 2019: highlights
- Wang P, Deng X, Zhou H, Yu S (2019) Estimates of the social cost of carbon: a review based on meta-analysis. J Clean Product 209:1494–1507 Google Scholar
- Weitzman ML (2009) On modeling and interpreting the economics of catastrophic climate change. Rev Econ Stat 91(1):1–19 Google Scholar
- Ye M, Wu J, Wang C, He X (2019) Historical and future changes in asset value and gdp in areas exposed to tropical cyclones in china. Weather Clim Soc 11(2):307–319 Google Scholar
- Yu Z, Wang Y, Xu H, Davidson N, Chen Y, Chen Y, Yu H (2017) On the relationship between intensity and rainfall distribution in tropical cyclones making landfall over china. J Appl Meteorol Climatol 56(10):2883–2901 Google Scholar
- Zhao M, Zhou Y, Li X, Cao W, He C, Yu B, Li X, Elvidge CD, Cheng W, Zhou C (2019) Applications of satellite remote sensing of nighttime light observations: advances, challenges, and perspectives. Remote Sens 11 (17):1971 Google Scholar
Funding
Open access funding provided by University of Bern.
This article appeared on the Climatic Change website at https://link.springer.com/article/10.1007/s10584-020-02810-6
]]>